[아이티윌 빅데이터 52기] 비지도 학습 | 군집분석 | K MEANS 개요 | Iris 붓꽃 분류

비지도 학습 > 군집분석 > KMEANS > Iris 붓꽃 데이터 세트 활용

 

 

STEP 1. 데이터 세트 확인

 

 

 

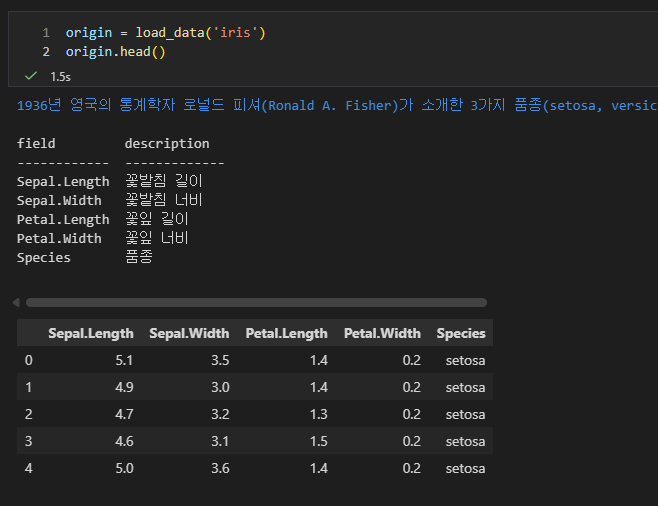
STEP 2 . 데이터 전처리

- 군집 분석은 종속 변수가 존재하지 않으므로, 종속변수를 제외하여 데이터 추출
- 만약 군집분석 후 나눠진 군집을 기존의 종속변수와 비교하려는 시도는 

  로지스틱 회귀 분석으로 통계량이 제공되는 과정이 더 나을수 있음

 

df= origin.drop('Species' , axis=1)
df.head()

 

 

 

STEP 3.K Means 의 하이퍼 파라미터

 

(1) Inertia : K MEANS 의 성능 평가 지표

- 각 데이터가 자신의 군집 중심까지 떨어진 거리의 제곱합
- 즉, 이 이너셔 값이 작을수록 각 데이터 포인트의 군집의 중심점을 기준으로 잘 뭉쳐있음을 의미
- 군집 내부 응집도 (군집 내부 압축 정도를 수치로 표현)
- 하지만 이너셔는 K 를 늘리면 무조건 줄어들기 떄문에 이녀셔가 작지만 K 가 너무 많지 않은 타협점을 찾아야하고, 그것이 엘보우 기법 (초반에는 급격하게 떨어지다가 어느순간 완만하게 줄어드는 지점을 찾아야함)

 

 

(2) k 의 변화에 따른 Inertia 값의 변화 시각화

klist = list(range(2,11))
inertia = [] # inertia 값을 저장할 리스트

for k in klist:
  estimator = KMeans(n_clusters = k , random_state=0)
  estimator.fit(X=df)
  inertia.append(estimator.inertia_)


inertia

# 1) 그래프 초기화
width_px = 1280              # 그래프 가로 크기
height_px = 720              # 그래프 세로 크기
rows = 1                     # 그래프 행 수
cols = 1                     # 그래프 열 수
my_dpi=200

figsize = (width_px / my_dpi, height_px / my_dpi)
fig, ax = plt.subplots(rows, cols, figsize=figsize, dpi=my_dpi)

# 2) Scatter Plot 그리기
sb.lineplot(x=klist, y=inertia, linestyle =':',marker ='o',markerfacecolor ='#0066ff' , markeredgecolor='#ffffff')

# 3) 그래프 꾸미기
ax.grid(True)                 # 배경 격자 표시/숨김

# 4) 출력
plt.tight_layout()            # 여백 제거
plt.show()                    # 그래프 화면 출력
plt.close()                   # 그래프 작업 종료

 

 

STEP 4. 엘보우 포인트로 적절한 k 값 찾아내기

-k 증가에 따른 이너셔 추세를 시각화하여 감소 폭이 급격 -> 완만으로 바뀌는 지점
이 지점이 최적의 k 값이 된다

 

 

KneeLocator 라이브러리 활용

#y 값이 감소하는 방향에서, 감소하는 볼록
kl = KneeLocator(klist,inertia,curve='convex',direction='decreasing')

best_k = kl.elbow   #최적의 k 값 출력
best_y=kl.elbow_y   #최적의 inertia 값 출력

print('found elbow' , best_k)
print('found y:' , best_y)

 

- Kneed 라이브러리의 KneeLocator 를 써서 ELBOW 지점을 자동으로 찾아주는 방법
- klist 와 inertia 를 입력하면 최적의 k 와 그때의 inertia 값을 출력함

 

 

 

STEP 5. 클러스터링 시각화

- 클러스터링 된 값을 컬럼으로 추가해줌

estimator = KMeans(n_clusters=best_k)  #모델 객체 생성
estimator.fit(df) #모델 학습

cluster =estimator.predict(df)  #예측
df['ClusterID'] = cluster
df

 

 

- 각 군집별로 색상을 칠해 경계선을 만들어주고, 각 군집의 중심점을 표현해줌

> 군집들이 겹쳐져 있는 이유 : 군집 분석 시 고려했던 컬럼 수는 4개인데, 현재 그래프는 2차원이다 보니 다른 변수들간의 관계가 보이지 않는것

vdf = df.copy()
hue_field ='ClusterID'
x_field ='Sepal.Length'
y_field = 'Sepal.Width'

# 1) 그래프 초기화
width_px = 1280              # 그래프 가로 크기
height_px = 720              # 그래프 세로 크기
rows = 1                     # 그래프 행 수
cols = 1                     # 그래프 열 수
my_dpi=200

figsize = (width_px / my_dpi, height_px / my_dpi)
fig, ax = plt.subplots(rows, cols, figsize=figsize, dpi=my_dpi)


#데이터 산점도
sb.scatterplot (data=vdf , x=x_field , y=y_field , hue=hue_field)



# 군집별 값의 종류별로 반복문 실행
for c in vdf[hue_field].unique():
  #값의 종류별로 데이터 프레임 구분
  df_c = vdf.loc[vdf[hue_field] == c , [x_field,y_field]]

  try:
    #외각선 좌표 계산
    hull = ConvexHull(df_c)

    #마지막 좌표 이후에 첫번쨰 좌표를 연결
    points = np.append(hull.vertices,hull.vertices[0])

    ax.plot( #type:ignore
      df_c.iloc[points,0] , df_c.iloc[points,1] , linewidth = 0.5 , linestyle =':'
      )
    
    ax.fill(df_c.iloc[points,0] , df_c.iloc[points ,1], alpha =0.1)


  except:
    pass

#군집별 중심점 표시
ax.scatter(
  estimator.cluster_centers_[:,0],
  estimator.cluster_centers_[:,1],
  marker='x',
  c='red',
  alpha=1,
  s=40
)


ax.grid(True ,alpha =0.3) #배경 격자 표시
plt.tight_layout()
plt.show()
plt.close()